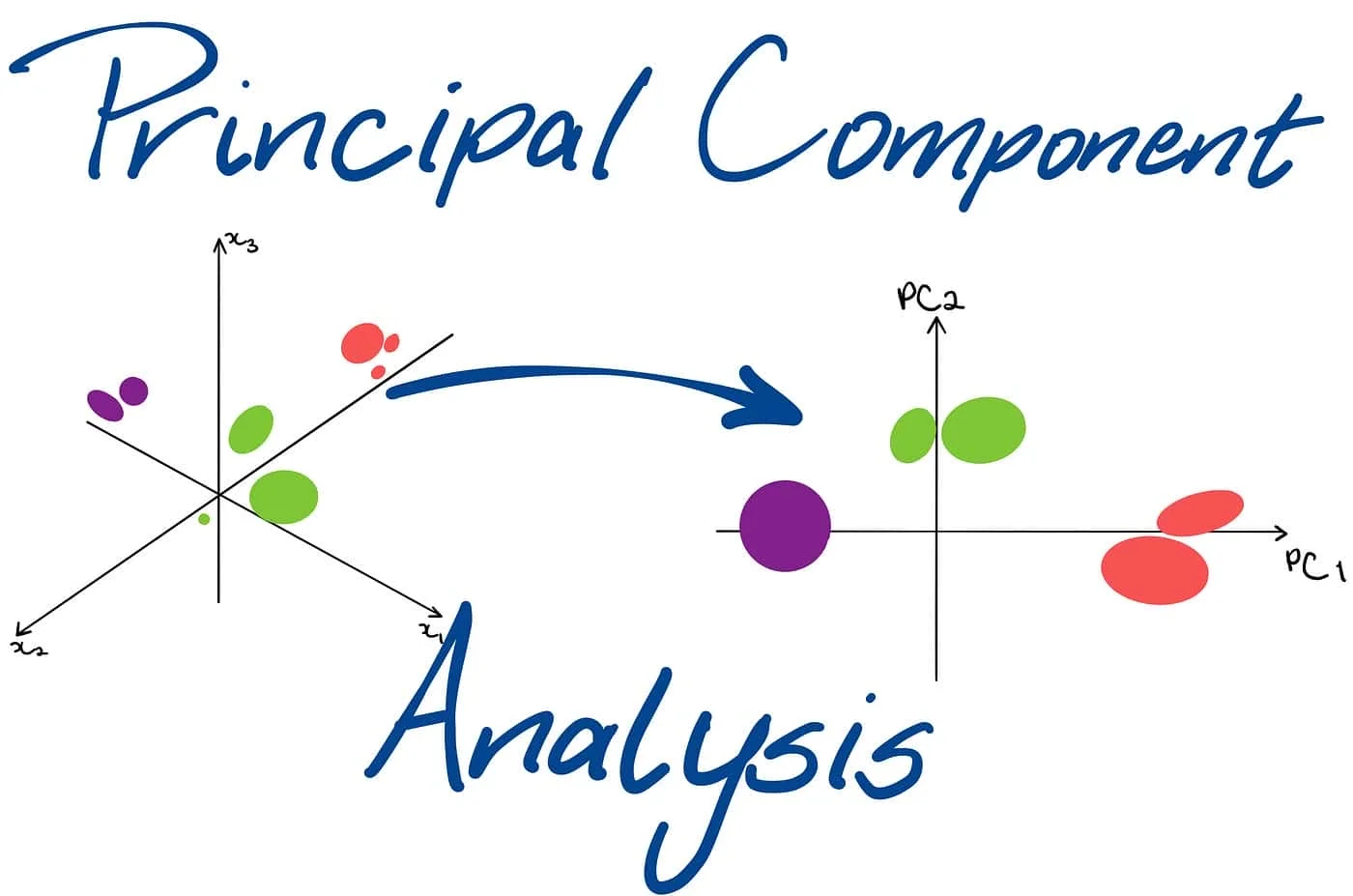
Machine learning heavily relies on data, where the abundance of data enhances model learning and prediction. However, this abundance presents a challenge known as the curse of dimensionality. Dealing with high-dimensional data can be complex and computationally expensive. Principal Component Analysis (PCA) emerges as a potent technique to address this challenge in machine learning.
PCA is part of a family of techniques designed to handle high-dimensional data by exploiting dependencies between variables to represent it in a more manageable, lower-dimensional form while preserving essential information. It is renowned for its simplicity and robustness, making it a popular choice for dimensionality reduction. Principal Component Analysis has a rich history and is known by various names like the Karhunen-Loève transformation, the Hotelling transformation, the method of empirical orthogonal functions, and singular value decomposition.
PCA is a multivariate technique specifically designed for analyzing data tables with inter-correlated quantitative variables describing observations. Its objective is to extract crucial information from the table, creating a set of new orthogonal variables called principal components. These components reveal the underlying patterns of similarity among observations and variables, facilitating better data representation and understanding. The efficacy of a Principal Component Analysis model can be assessed using cross-validation methods like bootstrap and jackknife. Additionally, PCA can be extended to handle qualitative variables through correspondence analysis (CA) and heterogeneous variable sets through multiple factor analysis (MFA). Mathematically, PCA relies on the eigen-decomposition of positive semidefinite matrices and the singular value decomposition (SVD) of rectangular matrices. In this article, we are going to deeply understand about What is Principal Component Analysis in Machine Learning and why it is important.
Understanding the Curse of Dimensionality
Imagine a vast, awe-inspiring landscape with towering mountains and deep valleys, symbolizing high-dimensional data in the realm of machine learning. This intricate terrain poses challenges akin to the curse of dimensionality, where traditional algorithms struggle to navigate and extract meaningful insights. Principal Component Analysis in Machine Learning emerges as a powerful tool to address these complexities.
In the realm of high-dimensional data, the problems are manifold:
- Escalating Training Time: As dimensions increase, training time escalates, demanding more computational resources.
- Data Sparsity: The abundance of dimensions leads to sparse data points, potentially compromising model accuracy.
- Overfitting Peril: Models risk memorizing training data without generalizing to new instances, leading to overfitting.
By leveraging PCA, a dimensionality reduction technique, one can mitigate these challenges:
- Identifying Significant Features: PCA aids in identifying the most significant features, reducing dimensionality while preserving essential information.
- Streamlining Training Processes: PCA streamlines training processes by reducing dimensionality, making models more efficient.
- Combating Data Sparsity and Overfitting: PCA helps combat data sparsity and overfitting, enhancing model performance in high-dimensional data analysis.
PCA to the Rescue: Unveiling the Core Concepts
PCA comes to the rescue by offering a dimensionality reduction technique. It simplifies complex, high-dimensional data by transforming it into a lower-dimensional space while retaining the most critical information. Let’s break down the key concepts behind PCA:
- Principal Components (PCs): These are new, uncorrelated features created by PCA. They capture the maximum variance in the original data, meaning they represent the directions of greatest spread in the data.
- Eigenvectors: These are mathematical constructs that define the directions of the principal components. They point along the axes of greatest variance in the data.
- Eigenvalues: These are numerical values associated with eigenvectors. They represent the amount of variance captured by each principal component. Higher eigenvalues correspond to principal components with more information.
Equations:


Here’s a table summarizing the key concepts of PCA:
| Concept | Description |
| Principal Components (PCs) | New uncorrelated features capturing maximum variance in the data. |
| Eigenvectors | Mathematical constructs defining directions of principal components. |
| Eigenvalues | Numerical values representing variance captured by each principal component. Higher values = more info. |
The PCA Workflow: A Step-by-Step Transformation
Principal Component Analysis (PCA) is a dimensionality reduction technique that transforms data into a lower-dimensional space while retaining most of the information. Here’s a detailed breakdown of the PCA workflow, incorporating software tools and real-world examples:
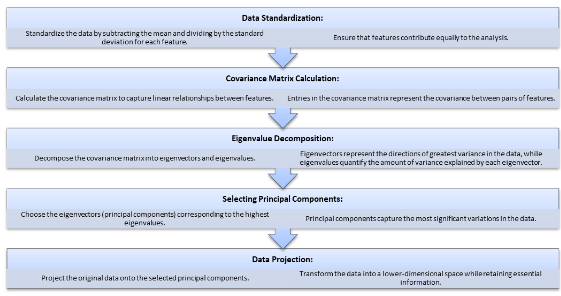
- Data Standardization (using Scikit-learn or R packages): PCA assumes features contribute equally. We standardize the data by subtracting the mean from each feature and then dividing by its standard deviation. Popular libraries like Scikit-learn (Python) or the ‘stats’ package in R provide functions like StandardScaler or scale to achieve this. For instance, in gene expression analysis, where each feature represents a gene’s expression level, standardization ensures variations in gene expression levels (due to factors like gene length) don’t overshadow underlying biological patterns.
- Covariance Matrix Calculation: The covariance matrix captures the linear relationships between each pair of features. It’s a square matrix where each entry represents the covariance between two corresponding features. Libraries like Scikit-learn (numpy.cov) or R (cov) can calculate the covariance matrix. In financial data analysis, the covariance matrix might reveal strong positive covariance between stocks in the same sector, indicating their price movements tend to be similar.
- Eigenvalue Decomposition (using Scikit-learn or MATLAB): This linear algebra technique decomposes the covariance matrix into its eigenvectors and eigenvalues. Eigenvectors represent the directions of greatest variance in the data, while eigenvalues quantify the amount of variance explained by each eigenvector. Scikit-learn’s PCA function (PCA) or MATLAB’s eigs function can be used for this step. Imagine a dataset of handwritten digits. The first principal component might capture the variation between thin and thick lines, identified through eigenvalue decomposition.
- Selecting Principal Components: Not all eigenvectors are equally important. We choose the eigenvectors (principal components) corresponding to the highest eigenvalues. These principal components capture the most significant variations in the data. Popular PCA implementations like Scikit-learn’s PCA or MATLAB’s PCA functions allow specifying the number of principal components to retain based on the explained variance ratio. For example, in image compression, we might choose the principal components capturing most of the image’s detail (like edges and textures), enabling us to discard less informative components for efficient compression.
- Data Projection: Finally, we project the original data points onto the chosen principal components. This effectively transforms the data into a lower-dimensional space spanned by these principal components. The projected data retains the most relevant information from the original data, but in a more compact form. Libraries like Scikit-learn (PCA.transform) or MATLAB’s PCA function (pca(X) followed by projection using the chosen components) can perform the projection.
By implementing principal component analysis software, we gain valuable insights from complex datasets like gene expression data (identifying major biological processes), financial data (revealing underlying trends and grouping similar stocks), and image data (enabling efficient compression). PCA not only reduces computational costs but also enhances visualization capabilities by allowing us to explore the data in a lower-dimensional space.
Unveiling the Benefits of Principal Component Analysis in Machine Learning
Principal Component Analysis machine learning presents a plethora of advantages for data scientists.
- Reduced Training Time: PCA excels at dimensionality reduction. By transforming data into a lower-dimensional space, PCA shrinks the number of features machine learning models need to process. This translates to significantly faster training times, allowing data scientists to iterate and experiment more efficiently.
- Improved Model Performance: PCA can act as a safeguard against overfitting. High-dimensional data can contain redundant information that confuses learning algorithms, leading to overfitting. PCA helps mitigate this by eliminating these redundancies and focusing on the most informative features. As a result, machine learning models trained on PCA-processed data often exhibit superior performance.
- Enhanced Data Visualization: High-dimensional data can be challenging to visualize effectively using traditional methods. PCA provides a solution by projecting the data onto a lower-dimensional space, typically 2D or 3D, enabling us to represent complex relationships graphically. This enhanced visualization empowers data scientists to gain deeper insights into the underlying structure of their data.
- Feature Selection: Through analysis of the principal components identified during PCA, data scientists can pinpoint which original features contribute most significantly to the overall data structure. This knowledge allows for informed feature selection, where less informative features can be discarded, leading to more efficient models and potentially uncovering previously hidden patterns.
Witnessing PCA in Action: Real-World Applications
Principal Component Analysis (PCA) transcends theory, finding practical applications in various machine learning domains:
- Image Compression: PCA acts as a data trimmer for images. By discarding less informative components identified through PCA, we can significantly reduce file size while preserving the essence of the image. This is crucial for efficient image storage and transmission.
- Recommendation Systems: PCA plays a key role in recommender systems. It helps analyze user behavior and product characteristics, uncovering underlying patterns. By identifying user preferences and product similarities through PCA, recommender systems can deliver more personalized and accurate suggestions.
- Anomaly Detection: PCA excels at establishing a “normal” data profile. Deviations from this baseline, identified through PCA analysis, might indicate anomalies. This has applications in fraud detection, where unusual spending patterns can be flagged, or predicting system failures by analyzing sensor data variations.
- Natural Language Processing (NLP): NLP tasks like sentiment analysis rely on word embeddings, numerical representations of words. PCA can be used to reduce the dimensionality of these embeddings, making them more computationally efficient while preserving the semantic relationships between words.
Understanding the Limitations of PCA
While powerful, PCA does have some limitations:
- Information Loss: PCA discards some information during dimensionality reduction. The choice of how many principal components to retain determines the information trade-off.
- Assumes Linear Relationships: PCA works best when the relationships between features are linear. In cases of complex, non-linear relationships, PCA might not be the most suitable technique.
- Interpretability of Principal Components: While principal components capture variance, interpreting their meaning in the context of
Conclusion: The Future of Principal Component Analysis in Machine Learning
Principal Component Analysis in Machine Learning remains a cornerstone technique for dimensionality reduction. Its ability to simplify complex data, improve model performance, and enhance visualization makes it a valuable tool for data scientists. As the field of machine learning continues to evolve, we can expect further advancements in PCA:
- Kernel PCA: This extension of PCA allows for handling non-linear relationships between features by mapping the data into a higher-dimensional space where linear relationships become evident.
- Sparse PCA: This variation focuses on identifying a sparse set of features that contribute most to the data’s structure, offering a more interpretable representation.
- Integration with Deep Learning: Combining PCA with deep learning architectures can lead to more powerful models that leverage the strengths of both techniques.
In conclusion, PCA remains a fundamental tool in the machine learning toolbox. With its ongoing development and integration with emerging techniques, PCA will continue to play a vital role in unlocking the potential of high-dimensional data for years to come.
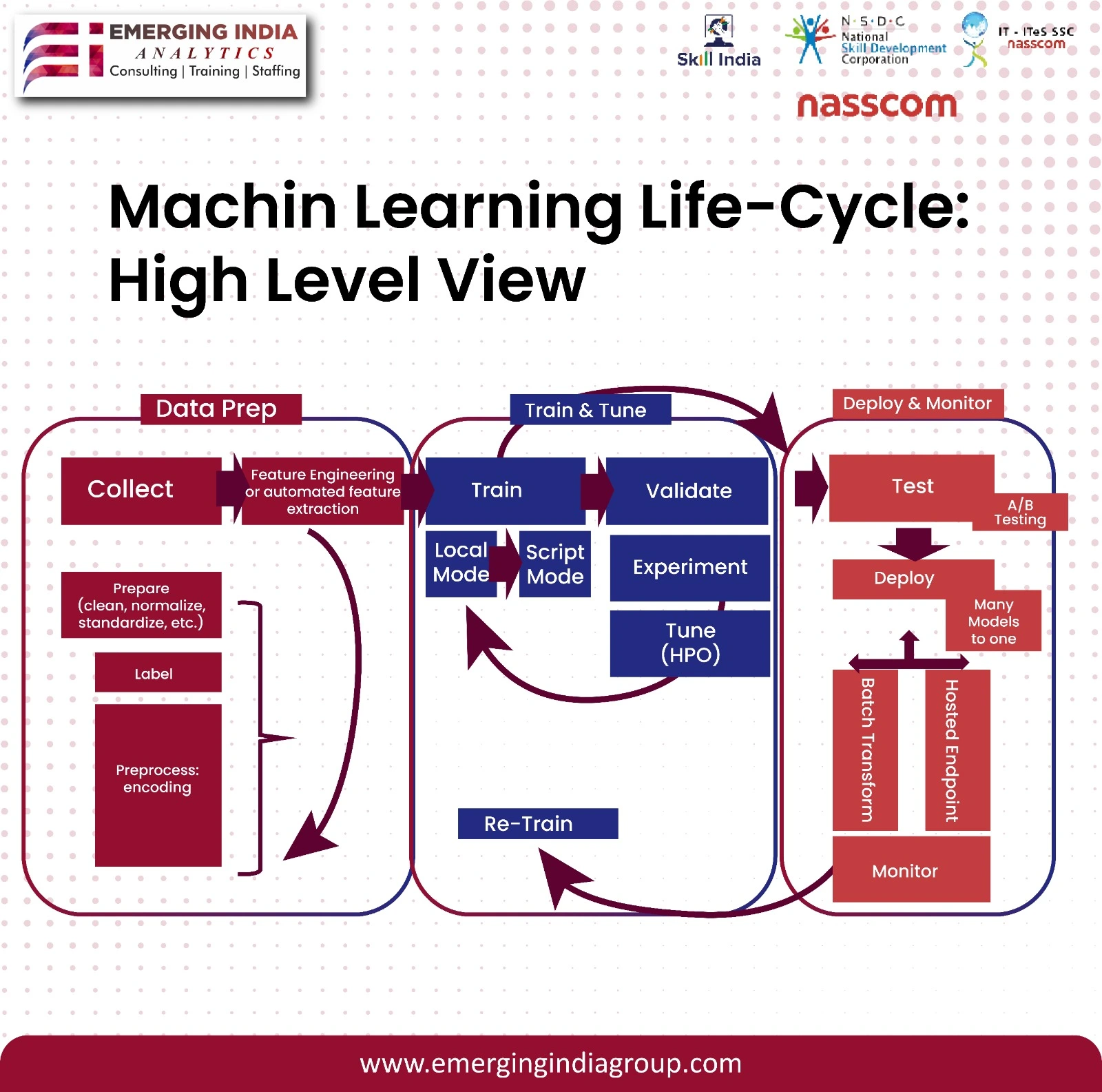
The diagram shows the different stages of the machine learning life cycle, including data preparation, training, and deployment.
- Data preparation involves collecting data, labeling data, and preprocessing data. Data preprocessing can include cleaning data, normalizing data, and standardizing data.
- Training involves training a machine learning model on the prepared data. The model learns from the data and is able to make predictions on new data.
- Deployment involves deploying the machine learning model to production. The model can then be used to make predictions on real-world data.
The diagram also shows that the machine learning life cycle is iterative. Once a model is deployed, it can be monitored and retrained on new data. This helps to improve the accuracy of the model over time.
Here are some additional details from the image:
- The data preparation stage includes collecting data, feature engineering, and preparing data.
- The training stage includes training, validating, and tuning the model.
- The deployment stage includes deploying the model to a local mode, script mode, or hosted endpoint.


